Tower of Hanoi (TOH) function call

Consider following algorithm (ignore syntax error)

void TOH(int n, int L, int R, int m)
if (n!=0)
{ TOH(n-1,L,R,m); // this part for recursion
   move from L to R;// Left to Right
   TOH(n-1,m,L,R); //this part for recursion 
}


Finding some values for n=1, n=2

1. total TOH() function call ?, 

2. total moves i.e. move from L to R ?, 

3. First move after how many TOH() call ? i.e. first move from L to R take place after some TOH() call,"

4. Similary for Last move after how many call ? i.e. last move from L to R take place after some TOH() call,


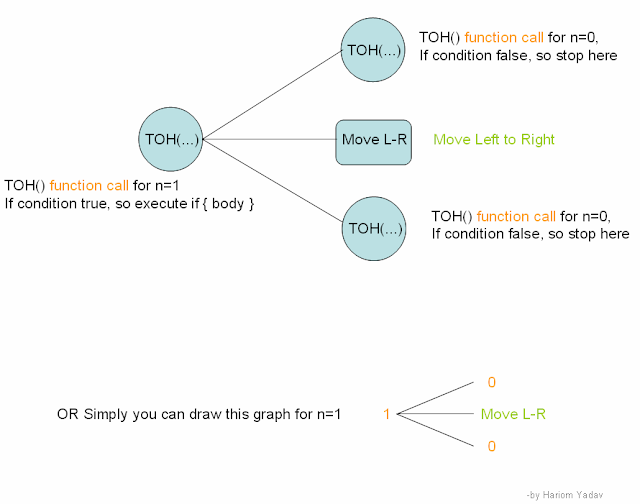
#1 Solving for n=1
step 1. Draw graph by using above TOH() function

Total TOH() function call for n=1
Method 1. 
See the graph above and count the total Orange color node+leaf i.e. 3 (1 root + 2 leaf)

Method 2.
Total TOH() call = 2^(n+1) - 1
Put n=1, we get 3

Total moves (moves L-R)
Method 1.
See the graph and count the total Green color leaf i.e. 1 [remember: Move L-R only contain leaf part since its not a function its a single body]

Method 2.
Total Move L-R = 2^n - 1
Put n=1, we get 1

First move L-R call after some TOH() call...
Method 1.
From graph we see that move L-R call after 2 TOH() call , 1st is node for n=1 and 2nd top TOH() for n=0 and after that move L-R call/execute

Method 2.
First move L-R after how many TOH() call = n + 1
Put n=1, we get 2

Similarly for last move L-R for this graph after how many TOH() call...
Method 1.
From graph we see that it is same as above, since there is only one move L-R take place

Method 2.
Last move L-R after how many TOH() call = Total TOH() call - 1 
                                                          = (2^(n+1) - 1)  - 1
Put n=1, we get 2

#2 Solving for n=2
step 1. Draw graph by using above TOH() function


Total TOH() function call for n=1
Total Orange color node+leaf i.e. 7 (1 root +2 node + 4 leaf)
or
Total TOH() call = 2^(n+1) - 1
Put n=2, we get 7


Total moves (moves L-R)
See the graph and count the total Green color leaf i.e. 3 
or
Total Move L-R = 2^n - 1
Put n=2, we get 3

First move L-R call after some TOH() call...
From graph we see that move L-R call after 3 TOH() call , see the small graph
or
First move L-R after how many TOH() call = n + 1
Put n=2, we get 3

Similarly for last move L-R for this graph after how many TOH() call...
See the graph we get last move take place after 6 TOH call
or
Last move L-R after how many TOH() call = Total TOH() call - 1 
                                                          = (2^(n+1) - 1)  - 1
Put n=2, we get 6